To solve this problem, let's break it down step-by-step:
Step 1: Calculate the Number of Triangles
To form a triangle, we need to select 3 points out of the 8 points on the circumference. The total number of triangles is given by the combination formula:
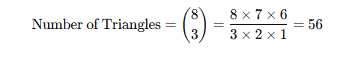
Step 2: Calculate the Number of Quadrilaterals
To form a quadrilateral, we need to select 4 points out of the 8 points on the circumference. The total number of quadrilaterals is:
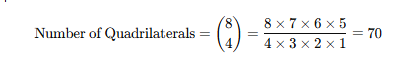
Step 3: Difference Between Quadrilaterals and Triangles
Now, we calculate the difference between the number of quadrilaterals and triangles:
Difference=70−56=14
Final Answer:
(1) 14